Answer:
Mean = 1.6
Variance = 0.84
Standard deviation = 0.916
Explanation:
We are given the following probability distribution below;
X P(X)
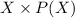

0 0.1 0 0
1 0.4 0.4 0.4
2 0.3 0.6 1.2
3 0.2 0.6 1.8
Total 1.6 3.4
Now, the mean of the probability distribution is given by;
Mean, E(X) =
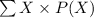 = 1.6
= 1.6
Also, the variance of the probability distribution is given by;
Variance, V(X) =
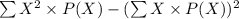
=
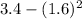
= 3.4 - 2.56 = 0.84
And the standard deviation of the probability distribution is given by;
Standard deviation, S.D. (X) =
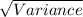
=
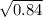 = 0.916.
= 0.916.