Question

Can you please help me with this

Answer 1

`\displaystyle A=(1)/(2)\int_\pi^{(7\pi)/(6)}{(cos(\theta)+sin(2\theta))^2}\,d\theta`

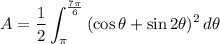
Explanation:

The shaded area is the area of the curve bounded by θ = π and θ = 7π/6.* A differential of area in polar coordinates is ...

dA = (1/2)r^2·dθ

So, the shaded area is ...

`\displaystyle\boxed{A=(1)/(2)\int_\pi^{(7\pi)/(6)}{(cos(\theta)+sin(2\theta))^2}\,d\theta}`

_____

* We found these bounds by trial and error using a graphing calculator to plot portions of the curve.