Question

The cold drawn AISI 1040 steel bar with 25-mm width and 10-mm thick has a 6- mm diameter thru hole in the center of the plate. The plate is subjected to a completely reversed axial load that fluctuates from 12kN to 28kN. Use notch sensitivity of 0.83.

Required:
a. Estimate the fatigue factor of safety based on yielding criteria.
b. Estimate the fatigue factor of safety based on Goodman and Morrow criteria.

Answer 1

A) ( N ) = 1.54

B) N ( Goodman ) = 1.133, N ( Morrow) = 1.35

Step-by-step explanation:

width of steel bar = 25-mm

thickness of steel bar = 10-mm

diameter = 6-mm

load on plate = between 12 kN AND 28 kN

notch sensitivity = 0.83

A ) Fatigue factor of safety based on yielding criteria

= δa + δm =
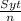`(Syt)/(n)` = 91.03 + 227.58 = 490 / N

therefore Fatigue number of safety ( N ) = 1.54

δa (amplitude stress ) = kf ( Fa/A) = 2.162 * ( 8*10^3 / 190 ) = 91.03 MPa

A = area of steel bar = 190 mm^2 , Fa = amplitude load = 8 KN , kf = 2.162

δm (mean stress ) = kf ( Fm/A ) = (2.162 * 20*10^3 )/ 190 = 227.58 MPa

Fm = mean load = 20 *10^3

B) Fatigue factor of safety based on Goodman and Morrow criteria

δa / Se + δm / Sut = 1 / N

= 91.03 / 183.15 + 227.58 / 590 = 1 /N

Hence N = 1.133 ( based on Goodman criteria )

note : Se = endurance limit (calculated) = 183.15 , Sut = 590

applying Morrow criteria

N = 1 / ( δa/Se) + (δm/ δf )

= 1 / ( 91.03 / 183.15 ) + (227.58 / 935 )

= 1.35