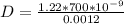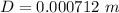Answer:
The distance is
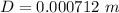
Step-by-step explanation:
From the question we are told that
The wavelength of the light source is
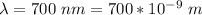
The distance from a pin hole is
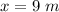
The diameter of the pin hole is
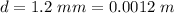
Generally the distance which the light source need to be in order for their diffraction patterns to be resolved by Rayleigh's criterion is
mathematically represented as
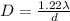
substituting values