Answer:
Explanation:
Hello, please consider the following.
First, assume that n equals
 . Therefore,
. Therefore,
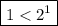 is
is

Next, assume that
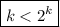 , as we attempt to prove
, as we attempt to prove
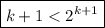
Since .... Therefore, we can conclude that
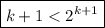
The choice for the last box is confusing. Based on your feedback, we can assume that we are still in the step 2 though.
And the last step which is not included in your question is the conclusion where we can say that we prove that for any integer
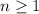 , we have
, we have
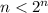 .
.
Hope this helps.
Do not hesitate if you need further explanation.
Thank you