Question

Assume that the returns from an asset are normally distributed. The average annual return for this asset over a specific period was 13.6 percent and the standard deviation of those returns in this period was 43.86 percent. a. What is the approximate probability that your money will double in value in a single year? (Do not round intermediate calculations and enter your answer as a percent rounded to 2 decimal places, e.g., 32.16.) b. What about triple in value? (Do not round intermediate calculations and enter your answer as a percent rounded to 6 decimal places, e.g., .161616.)

Answer 1

Answer: a. 2.44%

b. 0.001070%

Step-by-step explanation:

Given: The returns from an asset are normally distributed with

`\mu=\text{ 13.6 percent and }\sigma=\text{43.86 percent.}`

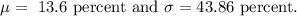
Let x be the percentage value of return.

a. Double in value in a single year i.e. 100% return.

z-value =
`(x-\mu)/(\sigma)`

`=(100-13.6)/(43.86)=1.97`

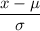
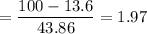
Required probability = Right-tailed probability for Z = 1.97

= 0.0244 [By p-value calculator]

= 2.44%

b. Triple in value in a single year i.e. 200% return.

z-value =
`(x-\mu)/(\sigma)`

`=(200-13.6)/(43.86)=4.25`

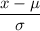
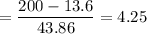
Required probability = Right-tailed probability for Z =4.25

= 0.0000107 [By p-value calculator]

= 0.001070%