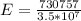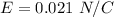Question

What is the magnitude of the applied electric field inside an aluminum wire of radius 1.4 mm that carries a 4.5-A current

Answer 1

Step-by-step explanation:

From the question we are told that

The radius is
`r = 1.4 \ mm = 1.4 *10^(-3) \ m`

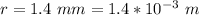
The current is
`I = 4.5 \ A`

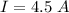
Generally the electric field is mathematically represented as

`E = (J)/(\sigma )`

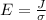
Where
`\sigma` is the conductivity of aluminum with value
`\sigma = 3.5 *10^(7) \ s/m`

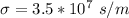
J is the current density which mathematically represented as

`J = (I)/(A)`

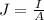
Here A is the cross-sectional area which is mathematically represented as

`A = \pi r^2`

`A = 3.142 * (1.4*10^(-3))^2`

`A = 6.158*10^(-6) \ m^2`

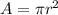
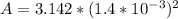
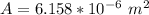
So

`J = ( 4.5 )/(6.158*10^(-6))`

`J = 730757 A/m^2`

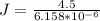
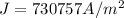
So

`E = ( 730757)/(3.5*10^(7) )`

`E = 0.021 \ N/C`