Answer:
Options (B) and (D)
Explanation:
If a triangle is a 30° - 60° - 90° triangle, measure of the angle between the leg and hypotenuse will be either 60° or 90°.
Therefore, by applying Cosine rule in the given options.
c² = a² + b² - 2abCosC
All the given options are the right triangles.
[Since they follow the Pythagoras theorem]
Option (A),
Angle between the sides having measures 3 and 5 units,
4² = 3² + 5² - 2(3)(5)CosC
16 = 9 + 25 - 30.CosC
30.CosC = 18
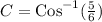
C = 33.56°
Therefore, this triangle is not a 30-60-90 triangle.
Option (B),
Angle between the sides measuring 5 and 10 units,
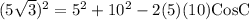
75 = 125 - 100(CosC)
Cos(C) = 0.5
C = 60°
Therefore, other angles of the triangle will be 30° and 90°.
And it's a 30°-60°-90° triangle.
Option (C),
10, 10, 10√2
It's a right triangle and the measure of legs are equal.
Since legs of this sides are equal, angles opposite to these equal sides will be equal.
Sum of all interior angles = 180°
m∠A + m∠B + m∠C = 180°
If m∠B = 90°
m∠A + 90° + m∠C = 180°
2(m∠A) = 90°
m∠A = 45°
Therefore, the given sides make a 45°- 45°- 90° triangle.
Option (D).
Angle between the sides 3 and 6,
(3√3)² = 3² + 6² -2(3)(6)CosC
27 = 9 + 36 - 36.(CosC)
CosC =

C =
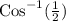
C = 60°
Therefore,
These sides make a 30°- 60°- 90° triangle.
Options (B) and (D) are the 30°- 60°- 90° triangle.