Answer:
![y = \sqrt[3]{4x+8}](https://img.qammunity.org/2021/formulas/mathematics/high-school/w1n35o13f984lif7hn9anumw74r8wwl03t.png)
All of 4x+8 is under a cube root sign.
=====================================================
Work Shown:
To find the inverse, we swap x and y, then solve for y.
![y = (1)/(4)x^3 - 2\\\\x = (1)/(4)y^3 - 2\\\\x+2 = (1)/(4)y^3\\\\4(x+2) = y^3\\\\4x+8 = y^3\\\\y^3 = 4x+8\\\\y = \sqrt[3]{4x+8}\\\\](https://img.qammunity.org/2021/formulas/mathematics/high-school/rckb0yl255yjzj2d670nt3np4klpmd8pdw.png)
------------
Side note:
If
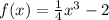 and
and
![g(x) = \sqrt[3]{4x+8}](https://img.qammunity.org/2021/formulas/mathematics/high-school/j7b4dm2jpmpsie14solmoseebqosb79q1d.png) , then
, then
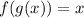 and
and
 for all x values in the domain. Effectively, you use function composition to confirm that we have the correct inverse equation.
for all x values in the domain. Effectively, you use function composition to confirm that we have the correct inverse equation.