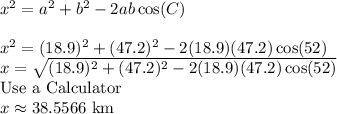Question

Starting at point​ A, a ship sails 18.9 km on a bearing of 190 degrees and ​then turns and sails 47.2km on a bearing of 318 degrees. Find the distance of the ship from point A. (Use trigonometry)

Answer 1

Approximately 38.56 kilometers

Explanation:

So, from the picture, we want to find x.

To do this, we can use the Law of Cosines. We simply need to find the angle between the two sides and then plug them into the Law of Cosines. First, the Law of Cosines is:

`c^2=a^2+b^2-2ab\cos(C)\\`

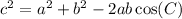
The c in this equation is our x, and the C is the angle we need to find.

From the picture, you can see that angle C is the sum of the red and blue angles.

From a bearing of 190 degrees, we can determine that the red angle measures 10 degrees. Then by alternate interior angles, the other red angle must also measure 10 degrees.

From a bearing of 318 degrees, the remaining 48 degrees is outside the triangle. However, we have a complementary angle, so we can find the angle inside the triangle by subtracting in into 90. Therefore, the blue angle inside is 90-48=42 degrees.

Therefore, angle C is 42+10 which equals 52 degrees. Now we can plug this into our formula:

`x^2=a^2+b^2-2ab\cos(C)\\\\x^2=(18.9)^2+(47.2)^2-2(18.9)(47.2)\cos(52)\\x=√((18.9)^2+(47.2)^2-2(18.9)(47.2)\cos(52))\\\text{Use a Calculator}\\x\approx38.5566 \text{ km}`