Answer:
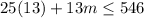
A
Explanation:
Each team can only consists of thirteen players. Therefore, by letting w represent the number of women's teams and m the number of men's teams, the total number of players is represented by the equation:
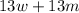
The total number of players cannot surpass 546. In other words, it must be less than or equal to. Therefore:
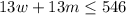
We are given that that 25 women's teams have already signed up. To find out the possible number of men's teams that can sign up, we can substitute 25 for w and then solve for m.
Therefore:
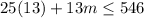
In conclusion, the answer is A.