Question

Find the mean, median, and mode

Answer 1

Mean = $70.8

Median = $70

Mode = $60

Explanation:

From the line plot attached,

Prices of the sunglasses are,

$20, $20, $50, $50, $50, $60, $60, $60, $60, $60, $60, $70, $70, $70, $80, $80, $80, $80, $90, $90, $90, $90, $100, $100, $130

Since mean of the data = Average of the terms

`=\frac{\text{Sum of the terms in the data set}}{\text{Number of terms}}`

=
`(2(20)+3(50)+6(60)+3(70)+4(80)+4(90)+2(100)+130)/((2+3+6+3+4+2+1))`

=
`(40+150+360+210+320+360+200+130)/(25)`

=
`(1770)/(25)`

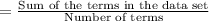
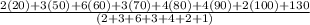
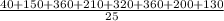
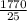
= $70.8

Median = Middle term of the data set

Since number of terms of the data set are odd (25)

Therefore, median =
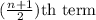`((n+1)/(2))\text{th term}` [where n = number of terms in the data set]

=
`(25+1)/(2)`

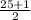
= 13th term

13th term of the data set is $70.

Therefore, Median = $70

Mode = Term repeated the most

In the data set $60 is the term which is repeated the most (6 times).

Therefore, Mode = $60