Answer:
sin(θ) = (2/5)√6
Explanation:
The sine and cosine are related by the formula ...

Filling in the given value for cos(θ), we find the sine to be ...
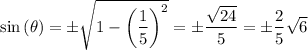
__
The cosine function is positive for angles in both the first and fourth quadrants. The restriction on θ tells us this is a first-quadrant angle. The sine is positive in the first quadrant, so the desired value is ...
sin(θ) = (2/5)√6