Question

a ball is dropped from a height of 512 inches onto a level floor. after the fourth bounce it is still 2 inches off the ground. presuming that the height the ball bounces is always the same fraction of the height reached on the previous bounce. what is that fraction? A) 1/4 B) 3/7 C) 5/9 D)4/7 E)3/5

Answer 1

A. 1/4.

Explanation:

This is exponential decay so we have , where x = the fraction:

512(x)^4 = 2

x^4 = 1/256

x= 1 / (256)^0.25

= 1/4

Answer 2

A. 1/4

Explanation:

We know that before the 1st bounce, the height of the ball is 512 inches.

Say the fraction is x.

Then, after the first bounce, the height of the ball is 512 * x = 512x.

After the second bounce, the height is now x * 512x = 512x².

By similar reasoning, the height after the third bounce is 512x³ and after the fourth bounce, it is
`512x^4`.

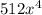We also know that after the fourth bounce, the height is 2 inches. So, set 2 equal to
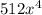`512x^4`:

2 =
`512x^4`

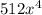
Divide both sides by 512:

`x^4=2/512`
`x^4=2/512=1/256`

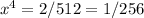
Take the fourth root of both sides:

`x=\sqrt[4]{1/256} =1/4`

Hence, the answer is A.

~ an aesthetics lover