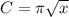Question

If a square has an area of x, then, in terms of x, what is the circumference of the largest circle that can be inscribed in the square? Answer: pi square root x AKA π√ x This is an SAT Math question no CALCULATOR. Show all the work

Answer 1

See below.

Explanation:

Assign the variable n to be the sides of the square.

Since a square has four equal sides, the area of the square is n^2 or x.

Therefore:

`n=√(x)`

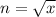
The largest circle that can be inscribed in the square will have the largest possible diameter. The largest possible diameter will be straight across the center of the circle. So, the largest possible diameter will be the side length, n.

Therefore, the radius will be n/2.

The circumference of a circle is:

`C=2\pi r`

Plug in n/2 for the radius:

`C=2\pi ((n)/(2))\\ C=n\pi`

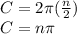
Now, substitute n for the square root of x:

`C=\pi√(x)`

Answer 2

C = pi sqrt(x)

Explanation:

The area of a square is x

A = s^2 where s is the side length

x = s^2

Take the square root of each side

sqrt(x) = s

This would be the diameter of the inscribed circle

The circumference of a circle is given by

C = pi d

C = pi sqrt(x)