Answer:
b = 9.5 , c = 15
Explanation:
For b
To find side b we use the sine rule
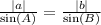
a = 7
A = 23°
B = 32°
b = ?
Substitute the values into the above formula
That's

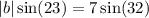
Divide both sides by sin 23°
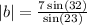
b = 9.493573
b = 9.5 to the nearest tenth
For c
To find side c we use sine rule
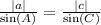
C = 125°
So we have
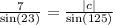
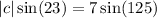
Divide both sides by sin 23°
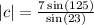
c = 14.67521
c = 15.0 to the nearest tenth
Hope this helps you