Question

PLS HELP:Find all the missing elements:

Answer 1

b = 9.5 , c = 15

Explanation:

For b

To find side b we use the sine rule

`( |a| )/( \sin(A) ) = ( |b| )/( \sin(B) )`

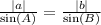
a = 7

A = 23°

B = 32°

b = ?

Substitute the values into the above formula

That's

`(7)/( \sin(23) ) = ( |b| )/( \sin(32) )`

`|b| \sin(23) = 7 \sin(32)`

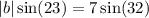
Divide both sides by sin 23°

`|b| = (7 \sin(32) )/( \sin(23) )`

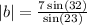
b = 9.493573

b = 9.5 to the nearest tenth

For c

To find side c we use sine rule

`( |a| )/( \sin(A) ) = ( |c| )/( \sin(C) )`

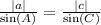
C = 125°

So we have

`(7)/( \sin(23) ) = ( |c| )/( \sin(125) )`

`|c| \sin(23) = 7 \sin(125)`

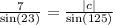
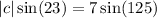
Divide both sides by sin 23°

`|c| = (7 \sin(125) )/( \sin(23) )`

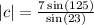
c = 14.67521

c = 15.0 to the nearest tenth

Hope this helps you