Question

Prove that (3-4sin^2)(1-3tan^2)=(3-tan^2)(4cos^2-3)

Answer 1

Proof in the explanation.

Explanation:

I expanded both sides as a first step. (You may use foil here if you wish and if you use that term.)

This means we want to show the following:

`3-9\tan^2(\theta)-4\sin^2(\theta)+12\sin^2(\theta)\tan^2(\theta)`

`=12\cos^2(\theta)-9-4\cos^2(\theta)\tan^2(\theta)+3\tan^2(\theta)`.

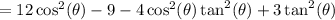After this I played with only the left hand side to get it to match the right hand side.

One of the first things I notice we had sine squared's on left side and no sine squared's on the other. I wanted this out. I see there were cosine squared's on the right. Thus, I began with Pythagorean Theorem here.

`3-9\tan^2(\theta)-4\sin^2(\theta)+12\sin^2(\theta)\tan^2(\theta)`

`3-9\tan^2(\theta)-4(1-\cos^2(\theta))+12\sin^2(\theta)\tan^2(\theta)[tex]</p><p>Distribute:</p><p>[tex]3-9\tan^2(\theta)-4+4\cos^2(\theta)+12\sin^2(\theta)\tan^2(\theta)`

Combine like terms and reorder left side to organize it based on right side:

`4\cos^2(\theta)-1+12\sin^2(\theta)\tan^2(\theta)-9\tan^2(\theta)`

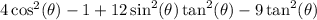
After doing this, I since that on the left we had products of sine squared and tangent squared but on the right we had products of cosine squared and tangent squared. This problem could easily be fixed with Pythagorean Theorem again.

`4\cos^2(\theta)-1+12\sin^2(\theta)\tan^2(\theta)-9\tan^2(\theta)`

`4\cos^2(\theta)-1+12(1-\cos^2(\theta))\tan^2(\theta)-9\tan^2(\theta)`

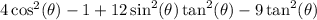
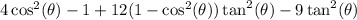
Distribute:

`4\cos^2(\theta)-1+12\tan^2(\theta)-12\cos^2(\theta)\tan^2(\theta)-9\tan^2(\theta)`

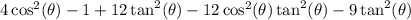
Combined like terms while keeping the same organization as the right:

`4\cos^2(\theta)-1+3\tan^2(\theta)-12\cos^2(\theta)\tan^2(\theta)-9\tan^2(\theta)`

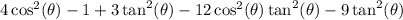
We do not have the same amount of the mentioned products in the previous step on both sides. So I rewrote this term as a sum. I did this as follows:

`4\cos^2(\theta)-1+3\tan^2(\theta)-12\cos^2(\theta)\tan^2(\theta)-9\tan^2(\theta)`

`4\cos^2(\theta)-1+3\tan^2(\theta)-4\cos^2(\theta)\tan^2(\theta)-8\cos^2(\theta)\tan^2(\theta)-9\tan^2(\theta)`

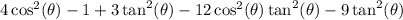
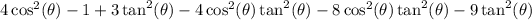
Here, I decide to use the following identity
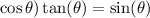`\cos\theta)\tan(\theta)=\sin(\theta)`. The reason for this is because I certainly didn't need those extra products of cosine squared and tangent squared as I didn't have them on the right side.

`4\cos^2(\theta)-1+3\tan^2(\theta)-4\cos^2(\theta)\tan^2(\theta)-8\cos^2(\theta)\tan^2(\theta)-9\tan^2(\theta)`

`4\cos^2(\theta)-1+3\tan^2(\theta)-4\cos^2(\theta)\tan^2(\theta)-8\sin^2(\theta)-9\tan^2(\theta)`

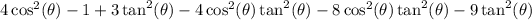
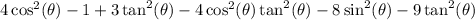
We are again back at having sine squared's on this side and only cosine squared's on the other. We will use Pythagorean Theorem again here.

`4\cos^2(\theta)-1+3\tan^2(\theta)-4\cos^2(\theta)\tan^2(\theta)-8\sin^2(\theta)-9\tan^2(\theta)`

`4\cos^2(\theta)-1+3\tan^2(\theta)-4\cos^2(\theta)\tan^2(\theta)-8(1-\cos^2(\theta))-9\tan^2(\theta)`

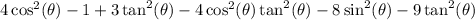
Distribute:

`4\cos^2(\theta)-1+3\tan^2(\theta)-4\cos^2(\theta)\tan^2(\theta)-8+8\cos^2(\theta)-9\tan^2(\theta)`

Combine like terms:

`12\cos^2(\theta)-9+3tan^2(\theta)-4\cos^2(\theta)\tan^2(\theta)`

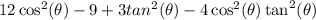
Reorder again to fit right side:

`12\cos^2(\theta)-9+4\cos^2(\theta)\tan(\theta)+3\tan^2(\theta)`

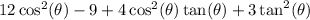
This does match the other side.

The proof is done.

Note: Reordering was done by commutative property.