Question

A uniform horizontal beam with a length of 8m and weigh of 200N is attached to a wall by a pin connection ..Its far end is supported by the cable tha makes an angle of 53.0 with the beam. If 600N person stands 2m from the wall , find the tension in the cable as well as the magnitude and direction of the force exerted by the wall on the beam.

Answer 1

The tension in the cable is approximately 1440.0 N

Step-by-step explanation:

The length of the beam = 8 m

The weight of the beam = 200 N

The angle made by the beam support cable = 53°

The weight of the person = 600 N

The position where the person stands = 2 m

The forces acting are the weight of the cable acting at the center of the beam and the weight of the person acting at 2 m from the wall

Therefore, we have;

Sum of moments = 0, which gives;

2000 × 4 + 2 × 600 - 8 ×
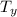`T_y` = 0

2000 × 4 + 2 × 600 = 8 ×
`T_y`

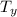
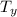`T_y` = 9200/8 = 1150 N

The tension in the cable, T = The component of the force in the cable

The vertical component of the tension
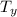`T_y` = T×sin(53)

Therefore;

T =
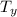`T_y`/(sin(53)) = 1150/(sin(53 degrees)) = 1439.96 ≈ 1440 N

The tension in the cable, T is approximately 1440 N.