Question

Is △FHK similar to △GHJ? If so, which postulate or theorem proves these two triangles are similar? ​△FHK​ ​ is similar to ​ ​△GHJ​ ​ by the ​ ​SSS Similarity Theorem​. ​△FHK​ ​ is similar to ​ ​△GHJ​ ​ by the ​SSA Similarity Theorem​. ​△FHK​ ​ is similar to ​ ​△GHJ​ ​ by the ​ ​ ​SAS Similarity Theorem. ​△FHK​ ​ is not similar to ​ ​△GHJ​​.

Answer 1

ΔFHK and ΔGHJ are the similar triangles by SAS similarity theorem.

Explanation:

Picture for the given question is missing; find the picture attached.

If
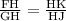`\frac{\text{FH}}{\text{GH}}=\frac{\text{HK}}{\text{HJ}}` and ∠H ≅ ∠H

Then ΔFHK ~ ΔGHJ

`\frac{\text{FH}}{\text{GH}}=\frac{\text{HK}}{\text{HJ}}`

`((12+10))/(10)=((15+18))/(15)`

`(22)/(10)=(33)/(15)`

`(11)/(5)=(11)/(5)`

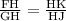
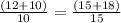
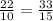
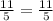
Since,
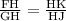`\frac{\text{FH}}{\text{GH}}=\frac{\text{HK}}{\text{HJ}}` and ∠H ≅ ∠H [By reflexive property]

Therefore, ΔFHK and ΔGHJ are the similar triangles by SAS similarity theorem.

Option (3) will be the answer.