Question

How do the number line graphs of the solutions sets of Negative 23 greater-than x and x greater-than-or-equal-to negative 23 differ?

Answer 1

the answer is A

Explanation:

Answer 2

For "Negative 23 greater-than x" , highlight the left half of the number line starting at -23 and use a parenthesis ) on -23.

For "x greater-than-or-equal-to negative 23", highlight the right half of the number line starting at -23, and use a square bracket [ on -23.

Explanation:

Start by locating the number -23 on the number line. Please see attached image to accompany the explanation.

In the first case: "Negative 23 greater-than x" , which is expressed mathematically as:

`-23 >x`

notice that "x" has to be strictly smaller than the number -23, therefore those sought x values must reside to the left of the number -23, so we have to highlight that half of the number line. Apart from that, we need to include a symbol on top of the number -23, that indicates that -23 itself shouldn't be considered as part of the set, that symbol is by convention a parenthesis ).

In the second case: "x greater-than-or-equal-to negative 23", which is expressed mathematically as:

`x\geq -23`

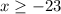
notice that "x" has to be greater than or equal to the number -23, therefore those sought x values must reside to the right of the number -23, so we have to highlight that half of the number line. Apart from that, we need to include a symbol on top of the number -23, that indicates that -23 itself should be considered as part of the set, that symbol is by convention a square bracket [.