Answer:

P(x ≤ 5 ) = 0.9707
P ( x ≥ 6) = 0.0293
Explanation:
The probability of a binomial mass distribution can be expressed with the formula:

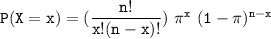
where;
n = 8 and π = 0.36
For x = 5
The probability
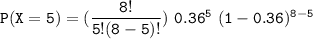
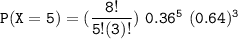
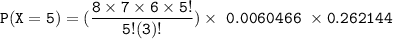
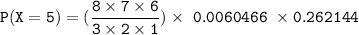
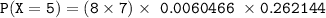
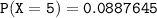
 to 4 decimal places
to 4 decimal places
b. x ≤ 5
The probability of P ( x ≤ 5)
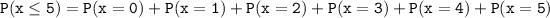
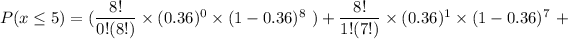

P(x ≤ 5 ) = 0.0281+0.1267+0.2494+0.2805+0.1972+0.0888
P(x ≤ 5 ) = 0.9707
c. x ≥ 6
The probability of P ( x ≥ 6) = 1 - P( x ≤ 5 )
P ( x ≥ 6) = 1 - 0.9707
P ( x ≥ 6) = 0.0293