Answer: -1 < x < 3
Explanation:
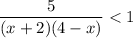
Step 1 The denominator cannot equal zero:
x + 2 ≠ 0 and 4 - x ≠ 0
x ≠ -2 4 ≠ x
Place these restrictive values on the number line with an OPEN dot:
<----------o-------------------o--------->
-2 4
Step 2 Find the zeros (subtract 1 from both sides and set equal to zero):

Add the zeros to the number line with an OPEN dot (since it is <):
<----------o-----o----------o----o--------->
-2 -1 3 4
Step 3 Choose test points to the left, between, and to the right of the points plotted on the graph. Plug those values into (x - 3)(x + 1) to determine its sign (+ or -):
Left of -2: Test point x = -3: (-3 - 3)(-3 + 1) = Positive
Between -2 and -1: Test point x = -1.5: (-1.5 - 3)(-1.5 + 1) = Positive
Between -1 and 3: Test point x = 0: (0 - 3)(0 + 1) = Negative
Between 3 and 4: Test point x = 3.5: (3.5 - 3)(3.5 + 1) = Positive
Right of 4: Test point x = 5: (5 - 3)(5 + 1) = Positive
+ + - + +
<----------o-----o----------o----o--------->
-2 -1 3 4
Step 4 Determine the solution(s) based on the inequality symbol. Since the original inequality was LESS THAN, we want the solutions that are NEGATIVE.
Negative values only occur between -1 and 3
So the solution is: -1 < x < 3