Answer:
(a). x = 80°
(b). x = 7.2 units
Explanation:
Angle formed between the tangents from a point outside the circle measure the half of the difference of intercepted arcs.
(a). Here the intercepted arcs are,
Measure of major arc = 360° - 100°
= 260°
Measure of minor arc = 100°
x° =
![(1)/(2)[m(\text{Major arc})-m(\text{Minor arc})]](https://img.qammunity.org/2021/formulas/mathematics/college/equ3raowrng6ze5fwbrc9azrx01cfond0a.png)
=
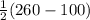
x = 80°
(b). If a secant and tangent are drawn form a point outside the circle, then square of the measure of tangent is equal to the product of the measures of the secant segment and and its external segment.
x² = 4(4 + 9)
x² = 4 × 13
x² = 52
x = √52
x = 7.211 ≈ 7.2 units