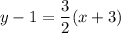Question

5

What is the equation, in point-slope form, of the line that
is parallel to the given line and passes through the point
(-3, 1)?
4
3
2
(-3, 1)
42.27
1
5 4 3 2 1
2 3 4 5 x
y-1=-{(x+3)
y-1=-{(x + 3)
y-1= {(x + 3)
y-1= {(x + 3)
(-2, 4)

Answer 1

Answer:
`y-1=\frac32(x+3)`

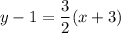
Explanation:

Slope of a line passes through (a,b) and (c,d) =
`(d-b)/(c-a)`

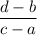
In graph(below) given line is passing through (-2,-4) and (2,2) .

Slope of the given line passing through (-2,-4) and (2,2) =
`(-4-2)/(-2-2)=(-6)/(-4)=(3)/(2)`

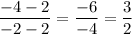
Since parallel lines have equal slope . That means slope of the required line would be .

Equation of a line passing through (a,b) and has slope m is given by :_

(y-b)=m(x-a)

Then, Equation of a line passing through(-3, 1) and has slope = is given by

`(y-1)=\frac32(x-(-3))\\\\\Rightarrow\ y-1=\frac32(x+3)`

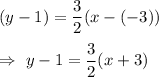
Required equation:
`y-1=\frac32(x+3)`