Question

Many elementary school students in a school district currently have ear infections. A random sample of children in two different schools found that 16 of 42 at one school and 18 of 34 at the other have ear infections. At the 0.05 level of significance, is there sufficient evidence to support the claim that a difference exists between the proportions of students who have ear infections at the two schools? Group of answer choices

Answer 1

Explanation:

The summary of the given data includes;

sample size for the first school
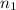`n_1` = 42

sample size for the second school
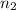`n_2` = 34

so 16 out of 42 i.e
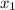`x_1` = 16 and 18 out of 34 i.e
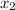`x_2` = 18 have ear infection.

the proportion of students with ear infection Is as follows:

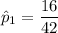`\hat p_1 = (16)/(42)` = 0.38095

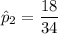`\hat p_2 = (18)/(34)` = 0.5294

Since this is a two tailed test , the null and the alternative hypothesis can be computed as :

`H_0 :p_1 -p_2 = 0 \\ \\ H_1 : p_1 - p_2 \\eq 0`

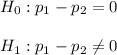
level of significance ∝ = 0.05,

Using the table of standard normal distribution, the value of z that corresponds to the two-tailed probability 0.05 is 1.96. Thus, we will reject the null hypothesis if the value of the test statistics is less than -1.96 or more than 1.96.

The test statistics for the difference in proportion can be achieved by using a pooled sample proportion.

`\bar p = (x_1 +x_2)/(n_1 +n_2)`

`\bar p = (16 +18)/(42 +34)`

`\bar p = (34)/(76)`

`\bar p = 0.447368`

`\bar p + \bar q = 1 \\ \\ \bar q = 1 -\bar p \\ \\\bar q = 1 - 0.447368 \\ \\\bar q = 0.552632`

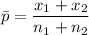
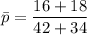
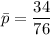
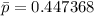
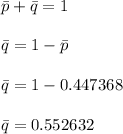
The pooled standard error can be computed by using the formula:

`S.E = \sqrt{ ( \bar p \bar q)/( n_1) + (\bar p \bar p)/(n_2) }`

`S.E = \sqrt{ ( 0.447368 * 0.552632)/( 42) + ( 0.447368 * 0.447368)/(34) }`

`S.E = \sqrt{ ( 0.2472298726)/( 42) + ( 0.2001381274)/(34) }`

`S.E = √( 0.01177284105)`

`S.E = 0.1085`

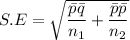
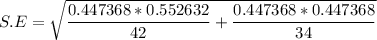
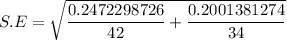
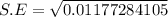
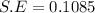
The test statistics is ;

`z = (\hat p_1 - \hat p_2)/(S.E)`

`z = (0.38095- 0.5294)/(0.1085)`

`z = (-0.14845)/(0.1085)`

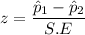
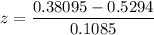
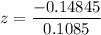
z = - 1.368

Decision Rule: Since the test statistics is greater than the rejection region - 1.96 , we fail to reject the null hypothesis.

Conclusion: There is insufficient evidence to support the claim that a difference exists between the proportions of students who have ear infections at the two schools