Question

Drag each tile to the correct box.

Answer 1

The order is 4) → 5) → 6) → 7) → 2) → 1) → 3)

Please find diagram with the arrangements

Explanation:

The horizontal width of an hyperbola

For

1)
`((y - 11)^2)/(7^2) -((x - 2)^2)/(6^2) = 1`

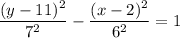
h = 2, k = 11

The widths are;

Horizontal (h - a, k) to (h + a, k) which is (2 - 7, 11) to (2 + 7, 11) = 14 units wide

(h, k - b) to (h, k + b) which is (2, 11 -6) to (2, 11 + 6) = 12 units wide

2)

`((y - 1)^2)/(5^2) -((x - 7)^2)/(12^2) = 1`

h = 7, k = 1

(h - a, k) to (h + a, k) which is (7 - 5, 1) to (7 + 5, 1) = Horizontal width 10 units wide

(h, k - b) to (h, k + b) which is (7, 1 -12) to (7, 1 + 12) = 24 units wide

3)
`((x - 6)^2)/(6^2) -((y + 1)^2)/(3^2) = 1`

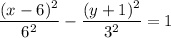
h = 6, k = -1

a = 8, b = 3

The widths are;

(6 - 8, -1) to (6 + 8, -1) Horizontal width = 16

(6, -1 - 3) to 6, -1 + 3) width = 6

4)
`((x - 4)^2)/(2^2) -((y + 2)^2)/(5^2) = 1`

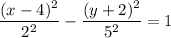
h = 4, k = -2, a = 2, b = 5

(4 - 2, (-2)) to (4 + 2, (-2)) Horizontal width = 4

(4, -2 - 5) to (4, -2 + 5) width = 10

5)
`((y + 5)^2)/(2^2) -((x + 4)^2)/(3^2) = 1`

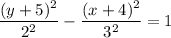
h = -4, k = -5, a = 2, b = 3

(-4 - 2, (-5)) to (-4 + 2, (-5)) Horizontal width = 4

(-4, -5 - 3) to (4, -5 + 3) width = 6

6)
`((y + 1)^2)/(2^2) -((x - 1)^2)/(9^2) = 1`

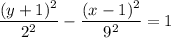
h = 1, k = -1, a = 2, b = 9

(1 - 2, (-1)) to (1 + 2, (-1)) Horizontal width = 4

(1, -1 - 9) to (1, -1 + 9) width = 18

7)
`((x + 7)^2)/(4^2) -((y - 9)^2)/(9^2) = 1`

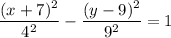
h = -7, k = 9, a = 4, b = 9

(-7 - 4, 9) to (-7 + 4, 9) Horizontal width = 8

(-7, 9 -9) to (-7, 9 + 9) width = 18