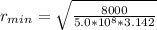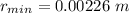Answer:
The radius is
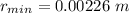
Step-by-step explanation:
From the question we are told that
The elastic limit(stress) is

The length is
The weight of the commercial sign is
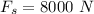
The maximum extension of the wire is

Generally the elastic limit of an alloy (stress) is is mathematically represented as
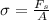
Where A is the cross-sectional area of the wire which is mathematically represented as
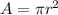
here
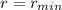 which is the minimum radius of the wire that support the commercial sign
which is the minimum radius of the wire that support the commercial sign
So
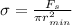
=>
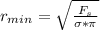
substituting values