Answer: 2.40
Explanation:
Given: The prices of 4 cars with similar characteristics that sold at a recent auction (in thousands of dollars): 6.6, 5, 10.7, 7.3.
Let x: 6.6, 5, 10.7, 7.3.
n= 4
Mean :
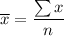
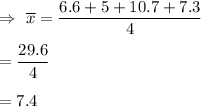
Now , standard deviation =
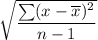
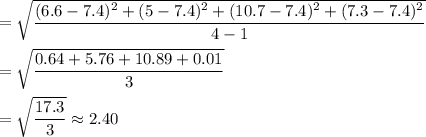
Hence, the standard deviation of the sample of selling prices = 2.40