Question

Need help pls will give you a good rating.

Answer 1

`\boxed{x + 4}`

Option C is the correct option

Step by step explanation

Let's find the expression which represents the length of the box:

`\mathsf{length * width * height \: of \: prism \: = \: volume \: of \: prism}`

`\mathsf{lengh * \: (x - 1) * (x + 8) = {x}^(3) + 11 {x}^(2) + 20x - 32}`

`\mathsf{length = \frac{ {x}^(3) + 11 {x}^(2) + 20x - 32 }{(x - 1)(x + 8)} }`

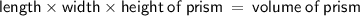
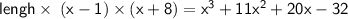
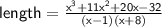
Write 11x² as a sum

`\mathsf{ = \frac{ {x}^(3) - {x}^(2) + 12 {x}^(2) + 20x - 32 }{(x - 1)(x + 8)} }`

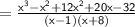
Write 20x as a sum

`\mathsf{ = \frac{ {x}^(3) - {x}^(2) + 12 {x}^(2) - 12x + 32x - 32 }{(x - 1)(x + 8)}}`

Factor out x² from the expression

`\mathsf{ = \frac{ {x}^(2)(x - 1) + 12 {x}^(2) - 12x + 32x - 32 }{(x - 1)(x + 8)} }`

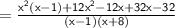
Factor out 12 from the expression

`\mathsf{ = \frac{ {x}^(2)(x - 1) + 12x(x - 1) + 32x - 32 }{(x - 1)(x + 8)} }`

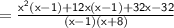
Factor out 32 from the expression

`\mathsf{ = \frac{ {x}^(2)(x - 1) + 12x(x - 1) + 32(x - 1) }{(x - 1)(x + 8)} }`

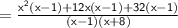
Factor out x+1 from the expression

`\mathsf{ = \frac{(x - 1)( {x}^(2) + 12x + 32) }{(x - 1)(x + 8)} }`

Factor out 12x as a sum

`\mathsf{ = \frac{(x - 1)( {x}^(2) + 8x + 4x + 32) }{(x - 1)(x + 8)} }`

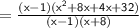
Reduce the fraction with x-1

`\mathsf{ = \frac{ {x}^(2) + 8x + 4x + 32 }{(x + 8)} }`

Factor out x from the expression

`\mathsf{ = (x(x + 8) + 4x + 32)/((x + 8)) }`

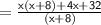
Factor out 4 from the expression

`\mathsf{ = (x(x + 8) + 4(x + 8))/(x + 8) }`

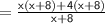
Factor out x+8 from the expression

`\mathsf{ = ((x + 8)(x + 4))/(x + 8) }`

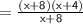
Reduce the fraction with x+8

`\mathsf{ = x + 4}`

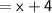
hence, x+4 is the expression that represents the length of a box.

Hope I helped!

Best regards!

Answer 2

x+4

.....................