Question

alculate the pH of the solution, upon addition of 0.035 mol of NaOH to the original buffer. Express your answer using two decimal places.

Answer 1

A 1.0-L buffer solution contains 0.100 mol HC2H3O2 and 0.100 mol NaC2H3O2. The value of Ka for HC2H3O2 is 1.8×10−5.

Calculate the pH of the solution, upon addition of 0.035 mol of NaOH to the original buffer.

Answer:

The pH of this solution = 5.06

Step-by-step explanation:

Given that:

number of moles of CH3COOH = 0.100 mol

volume of the buffer solution = 1.0 L

number of moles of NaC2H3O2 = 0.100 mol

The objective is to Calculate the pH of the solution, upon addition of 0.035 mol of NaOH to the original buffer.

we know that concentration in mole = Molarity/volume

Then concentration of [CH3COOH] =
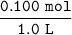`\mathtt{ (0.100 \ mol)/( 1.0 \ L )}` = 0.10 M

The chemical equation for this reaction is :

`\mathtt{CH_3COOH + OH^- \to CH_3COO^- + H_2O}`

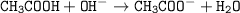
The conjugate base is CH3COO⁻

The concentration of the conjugate base [CH3COO⁻] is =
`\mathtt{ (0.100 \ mol)/( 1.0 \ L )}`

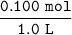
= 0.10 M

where the pka (acid dissociation constant)for CH3COOH = 4.74

If 0.035 mol of NaOH is added to the original buffer, the concentration of NaOH added will be =
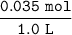`\mathtt{ (0.035 \ mol)/( 1.0 \ L )}` = 0.035 M

The ICE Table for the above reaction can be constructed as follows:

`\mathtt{CH_3COOH \ \ \ + \ \ \ \ OH^- \ \ \to \ \ CH_3COO^- \ \ \ + \ \ \ H_2O}`

Initial 0.10 0.035 0.10 -

Change -0.035 -0.035 + 0.035 -

Equilibrium 0.065 0 0.135 -

By using Henderson-Hasselbalch equation:

The pH of this solution = pKa + log
`\mathtt{(CH_3COO^-)/(CH_3COOH)}`

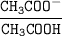
The pH of this solution = 4.74 + log
`\mathtt{(0.135)/(0.065)}`

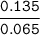
The pH of this solution = 4.74 + log (2.076923077 )

The pH of this solution = 4.74 + 0.3174

The pH of this solution = 5.0574

The pH of this solution = 5.06 to two decimal places