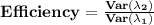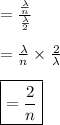Answer:
The answer is "
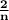 ".
".
Explanation:
considering
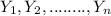 signify a random Poisson distribution of the sample size of n which means is λ.
signify a random Poisson distribution of the sample size of n which means is λ.
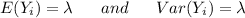
Let assume that,
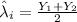
multiply the above value by Var on both sides:
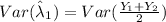
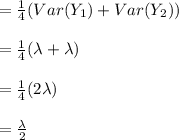
now consider
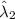 =
=
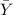
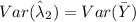
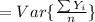
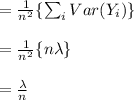
For calculating the efficiency divides the
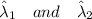 value:
value:
Formula: