Answer:
The edge length of a face-centered cubic unit cell is 435.6 pm.
Step-by-step explanation:
In a face-centered cubic unit cell, each of the eight corners is occupied by one atom and each of the six faces is occupied by a single atom.
Hence, the number of atoms in an FCC unit cell is:
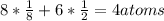
In a face-centered cubic unit cell, to find the edge length we need to use Pythagorean Theorem:
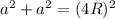 (1)
(1)
Where:
a: is the edge length
R: is the radius of each atom = 154 pm
By solving equation (1) for "a" we have:

Therefore, the edge length of a face-centered cubic unit cell is 435.6 pm.
I hope it helps you!