Question

What is the edge length of a face-centered cubic unit cell that is made of of atoms, each with a radius of 154 pm

Answer 1

The edge length of a face-centered cubic unit cell is 435.6 pm.

Step-by-step explanation:

In a face-centered cubic unit cell, each of the eight corners is occupied by one atom and each of the six faces is occupied by a single atom.

Hence, the number of atoms in an FCC unit cell is:

`8*(1)/(8) + 6*(1)/(2) = 4 atoms`

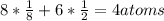
In a face-centered cubic unit cell, to find the edge length we need to use Pythagorean Theorem:

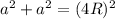`a^(2) + a^(2) = (4R)^(2)` (1)

Where:

a: is the edge length

R: is the radius of each atom = 154 pm

By solving equation (1) for "a" we have:

`a = 2R√(2) = 2*154 pm*√(2) = 435.6 pm`

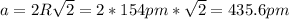
Therefore, the edge length of a face-centered cubic unit cell is 435.6 pm.

I hope it helps you!