Question

Two identical planets orbit a star in concentric circular orbits in the star's equatorial plane. Of the two, the planet that is farther from the star must have

Answer 1

The planet that is farther from the star must have a time period greater.

Step-by-step explanation:

We can determine the ratio of the period's planet with the radius of the circular orbit in the star's equatorial plane:

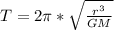`T = 2\pi*\sqrt{(r^(3))/(GM)}` (1)

Where:

r: is the radius of the circular orbit of the planet and the star

T: is the period

G: is the gravitational constant

M: is the mass of the planet

From equation (1) we have:

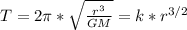`T = 2\pi*\sqrt{(r^(3))/(GM)} = k*r^(3/2)` (2)

Where k is a constant

From equation (2) we have that of the two planets, the planet that is farther from the star must have a time period greater.

I hope it helps you!