Question

Statistics professors believe the average number of headaches per semester for all students is more than 18. From a random sample of 15 students, the professors find the mean number of headaches is 19 and the standard deviation is 1.7. Assume the population distribution of number of headaches is normal.

Answer 1

Complete Question

Statistics professors believe the average number of headaches per semester for all students is more than 18. From a random sample of 15 students, the professors find the mean number of headaches is 19 and the standard deviation is 1.7. Assume the population distribution of number of headaches is normal.the correct conclusion at
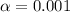`\alpha =0.001` is?

Answer:

There is no sufficient evidence to support the professor believe

Explanation:

From the question we are told that

The population mean is
`\mu = 18`

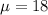
The sample size is
`n = 15`

The sample mean is
`\= x = 19`

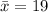
The standard deviation is
`\sigma = 1.7`

The level of significance is
`\alpha = 0.001`

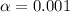
The null hypothesis is
`H_o: \mu = 18`

The alternative hypothesis is
`H_a : \mu > 18`

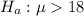
The critical value of the level of significance from the normal distribution table is

`Z_(\alpha ) = 3.290527`

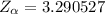
The test hypothesis is mathematically represented as

`t = (\= x - \mu )/( (\sigma)/( √(n) ) )`

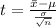
substituting values

`t = ( 19 - 18)/( (1.7)/( √(15) ) )`

`t = 2.28`

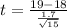
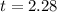
Looking at the value of t and
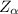`Z_(\alpha )` we can see that
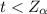`t < Z_(\alpha )` so we fail to reject the null hypothesis.

This mean that there is no sufficient evidence to support the professor believe