Question

Suppose you observed the equation for a traveling wave to be y(x, t) = A cos(kx − ????t), where its amplitude of oscillations was 0.15 m, its wavelength was two meters, and the period was 2/15 s. If a point on the wave at a specific time has a displacement of 0.12 m, what is the transverse speed of that point?

Answer 1

15m/s

Step-by-step explanation:

The equation for a traveling wave as expressed as y(x, t) = A cos(kx −
`\omega`t) where An is the amplitude f oscillation,
`\omega` is the angular velocity and x is the horizontal displacement and y is the vertical displacement.

From the formula;
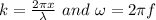`k =(2\pi x)/(\lambda) \ and \ \omega = 2 \pi f` where;

`\lambda \ is\ the \ wavelength \ and\ f \ is\ the\ frequency`

Before we can get the transverse speed, we need to get the frequency and the wavelength.

frequency = 1/period

Given period = 2/15 s

Frequency =
`(1)/((2/15))`

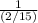
frequency = 1 * 15/2

frequency f = 15/2 Hertz

Given wavelength
`\lambda` = 2m

Transverse speed
`v = f \lambda`

`v = 15/2 * 2\\\\v = 30/2\\\\v = 15m/s`

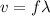
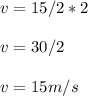
Hence, the transverse speed at that point is 15m/s