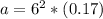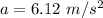Complete Question
The image of this question is shown on the first uploaded image
Answer:
a

b

c
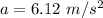
Step-by-step explanation:
From the question we are told that
The maximum displacement is A = 0.17 m
The time considered is
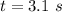
The spring constant is
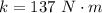
The mass is
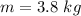
Generally given that the motion which the cylinder is undergoing is a simple harmonic motion , then the displacement is mathematically represented as
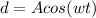
Where
 is the angular frequency which is mathematically evaluated as
is the angular frequency which is mathematically evaluated as
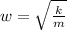
substituting values
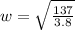
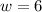
So the displacement is at t
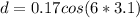

Generally the velocity of a SHM(simple harmonic motion) is mathematically represented as
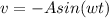
substituting values
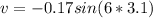

Generally the maximum acceleration is mathematically represented as

substituting values
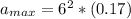
substituting values