Question

The same force is applied to two hoops. The hoops have the same mass, but the larger hoop has twice the radius. How are the angular accelerations of the hoops related

Answer 1

The angular accelerations of the hoops are related by the following equation
`\alpha _1 = 2\alpha_2`.

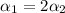Step-by-step explanation:

Net force on the hoop is given by;

`F_(net) = ma`

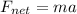
where;

a is linear acceleration

m is the mass

Net torque on the hoop is given by;

`\tau_(net) =I\alpha`

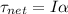
where;

I is moment of inertia

α is the angular acceleration

But, τ = Fr

`Fr = I \alpha\\\\\alpha = (Fr)/(I) \\\\\alpha = (Fr)/(mr^2) \\\\\alpha = (F)/(mr) \\\\\alpha = (1)/(r) ((F)/(m) )\\\\(since\ the \ force\ and \ mass \ are \ the \ same, (F)/(m) = constant=k)\\\\ \alpha = (k)/(r)\\\\k = \alpha r`

`\alpha _1 r_1= \alpha_2 r_2`

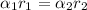
let the angular acceleration of the smaller hoop = α₁

let the radius of the smaller hoop = r₁

then, the radius of the larger loop, r₂ = 2r₁

let the angular acceleration of the larger hoop = α₂

`\alpha _1 r_1= \alpha_2 r_2\\\\\alpha_2= ( \alpha _1 r_1)/(r_2) \\\\\alpha_2=(\alpha _1 r_1)/(2r_1) \\\\\alpha_2= (\alpha _1)/(2) \\\\\alpha _1 = 2\alpha_2`

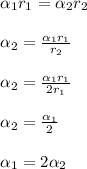
Therefore, the angular accelerations of the hoops are related by the following equation
`\alpha _1 = 2\alpha_2`