Question

Given the data: Ag2O(s), = ‑31.1 kJ mol-1, S° = +121.3 J mol-1 K-1 Ag(s), = 0.00 kJ mol-1, S° = +42.55 J mol-1 K-1 O2(g), = 0.00 kJ mol-1, S° = +205.0 J mol-1 K-1 Calculate the temperature at which = 0 for the reaction, Ag2O(s) → 2 Ag(s) + ½ O2(g). Assume that, since the physical states do not change, and are independent of tempera­ture between ‑50.0 °C and 950.0 °C.

Answer 1

`T=469.1K\\\\T=195.9\°C`

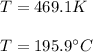
Step-by-step explanation:

Hello,

In this case, for the given decomposition reaction, we can compute the enthalpy of reaction considering the enthalpy of formation of each involved species (products minus reactants):

`\Delta _rH=2\Delta _fH_(Ag)+(1)/(2) \Delta _fH_(O_2)-\Delta _fH_(Ag_2O)\\\\\Delta _rH=2*0.00+(1)/(2) *0.00-(-31.1)=31.1kJ/mol`

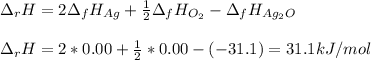
Next, the entropy of reaction considering the standard entropy for each involved species (products minus reactants):

`\Delta _rS=2S_(Ag)+(1)/(2) S_(O_2)-S_(Ag_2O)\\\\\Delta _rS=2(42.55)+(1)/(2) (205.0)-(121.3)=66.3J/(mol*K)`

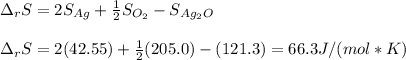
Next, since the Gibbs free energy of reaction is computed in terms of both the enthalpy and entropy of reaction at the unknown temperature, for such Gibbs energy equaling 0, the temperature (in K and °C) turns out:

`\Delta _rG=\Delta _rH-T\Delta _rS\\\\0=31.1kJ/mol-T(66.3(J)/(mol*K)*(1kJ)/(1000J) )\\\\T=(31.1kJ/mol)/(0.0663kJ/(mol*K)) =469.1K\\\\T=195.9\°C`

Which is within the given rank.

Best regards.