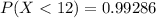Answer:
The probability is
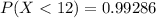
Explanation:
From the question we are told that
The population mean is
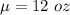
The standard deviation is
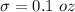
The sample mean is
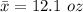
The sample size is n = 6 packs
The standard error of the mean is mathematically represented as
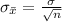
substituting values

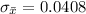
Given that the can’s contents follow a Normal distribution then then the probability that the mean contents of a six-pack are less than 12 oz is mathematically represented as
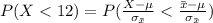
Generally
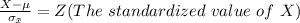
So
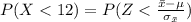
substituting values

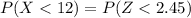
From the normal distribution table the value of
 is
is

=>