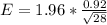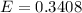Answer:
The margin of error is
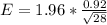
Explanation:
From the question we are told that
The sample size is

The sample mean is
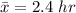
The standard deviation is
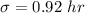
Given that the confidence level is 95% the the level of significance can be evaluated as
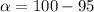
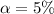
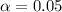
Next we obtain the critical value of
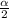 from the normal distribution table,the value is
from the normal distribution table,the value is
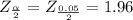
Generally the margin of error is mathematically represented as
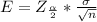
substituting values