Question

The head of a computer science department is interested in estimating the proportion of students entering the department who will choose the new computer engineering option. Suppose there is not information about the proportion of students who might choose the option. What size sample should the department head take if he wants to be 95% confident that the estimate is within 0.10 of the true proportion

Answer 1

96

Explanation:

From the given information:

At 95% Confidence interval level,Level of significance
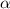`\alpha` 0.05, the value of Z from the standard normal tables = 1.96

Margin of Error = 0.10

Let assume that the estimated proportion = 0.5

therefore; the sample size n can be determined by using the formula:
`n =((Z)/(E))^2 * p* (1-p)`

`n =((1.96)/(0.1))^2 * 0.5* (1-0.5)`

`n =(19.6)^2 * 0.5* (0.5)`

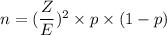
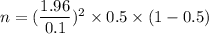
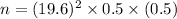
n = 96.04

n
`\approx` 96