Question

Heights of men on a baseball team have a​ bell-shaped distribution with a mean of and a standard deviation of . Using the empirical​ rule, what is the approximate percentage of the men between the following​ values? a.166 cm and 202 cm b. 172cm and 196cm

Answer 1

Let assume that the mean is 184 and the standard deviation is 6

Heights of men on a baseball team have a​ bell-shaped distribution with a mean 184 of and a standard deviation of 6 . Using the empirical​ rule, what is the approximate percentage of the men between the following​ values? a.166 cm and 202 cm b. 172 cm and 196cm

Answer:

P(156<X<202) = 99.7%

P(172<X<196) = 95.5%

Explanation:

Given that :

Heights of men on a baseball team have a​ bell-shaped distribution with a mean of and a standard deviation of . Using the empirical​ rule, what is the approximate percentage of the men between the following​ values? a.166 cm and 202 cm b. 172 cm and 196cm

For a.

Using the empirical​ rule, what is the approximate percentage of the men between the following​ values 166 cm and 202 cm.

the z score can be determined by using the formula:

`z = (X - \mu)/(\sigma)`

`z(166) = (166-184)/(6)`

`z(166) = (-18)/(6)`

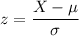
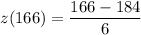
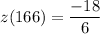
z(166) = -3

`z(202) = (202-184)/(6)`

`z(202) = (18)/(6)`

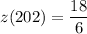
z(202) = 3

P(156<X<202) = P( μ - 3σ < X < μ + 3σ )

P(156<X<202) = P( - 3 < Z < 3)

P(156<X<202) = P( Z < 3) - P(Z < -3)

P(156<X<202) = 0.99865- 0.001349

P(156<X<202) = 0.997301

P(156<X<202) = 99.7%

For b.

b. 172 cm and 196cm

`z = (X - \mu)/(\sigma)`

`z(172) = (172-184)/(6)`

`z(172) = (-12)/(6)`

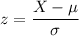
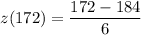
z(172) = -2

`z(196) = (196-184)/(6)`

`z(196) = (12)/(6)`

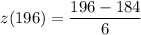
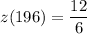
z(196) = 2

P(172<X<196) = P( μ - 2σ < X < μ + 2σ )

P(172<X<196) = P( - 2 < Z < 2)

P(172<X<196) = P( Z < 2) - P(Z < -2)

P(172<X<196) = 0.9772 - 0.02275

P(172<X<196) = 0.95445

P(172<X<196) = 95.5%