Answer:
the probability is 90% that the sample percentage is contained within 45.5% and 54.5% symmetric limits of the population percentage.
Explanation:
From the given information:
Sample size n = 200
The standard deviation for a sampling distribution for two brands are equally likely because the individual has no ability to discriminate between the two soft drinks.
∴
The population proportion
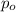 = 1/2 = 0.5
= 1/2 = 0.5
NOW;
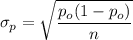
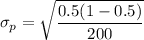
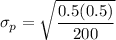

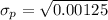
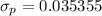
However, in order to determine the symmetrical limits of the population percentage given that the z probability is 90%.
we use the Excel function as computed as follows in order to determine the z probability = NORMSINV (0.9)
z value = 1.281552
Now the symmetrical limits of the population percentage can be determined as: ( 1.28, -1.28)

1.28 × 0.035355 = X - 0.5
0.0452544= X - 0.5
0.0452544 + 0.5 = X
0.5452544 = X
X
 0.545
0.545
X = 54.5%

- 1.28 × 0.035355 = X - 0.5
- 0.0452544= X - 0.5
- 0.0452544 + 0.5 = X
0.4547456 = X
X
 0.455
0.455
X = 45.5%
Therefore , we can conclude that the probability is 90% that the sample percentage is contained within 45.5% and 54.5% symmetric limits of the population percentage.