Answer:
Option (B)
Explanation:
1). Given function is,
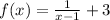
It the given function 'f' is transformed by a translation of 2 units to the right, the new function will be,
h(x) = f(x - 2)
h(x) =
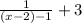
=
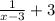
Further the new function is translated by 6 units down,
g(x) = h(x) - 6
g(x) =
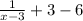
=
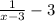
Since, transformed function 'g' passes through a point (x, -2),
g(x) =
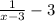
-2 =
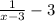
3 - 2 =
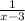
x - 3 = 1
x = 4
Therefore, Option (B) will be the answer.