Answer: HIJK is a parallelogram because the midpoint of both diagonals is (1,0) , which means the diagonals bisect each other.
Explanation:
Given: The coordinates of parallelogram H I J K as
H is at (- 2, 2), point I is at (4, 3), point J is at (4, - 2), and point K is at (- 2, - 3).
Diagonals : HJ and IK [join opposite vertices]
Mid point of HJ =
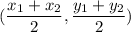
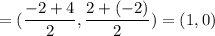
i.e. Mid point of HJ = (1,0)
Mid point of IK =
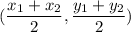
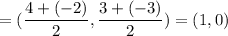
i.e. Mid point of IK = (1,0) =Mid point of HJ
When mid points of both diagonals are equal then that means the diagonals bisect each other.
Thus, HIJK is a parallelogram because the midpoint of both diagonals is (1,0) , which means the diagonals bisect each other.