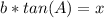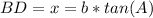In terms of the trigonometric ratios for ΔABD, what is the length of line segment BD?
Answer:
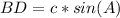
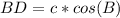
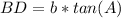
Explanation:
∆ABD is a right triangle.
Recall: trigonometric ratios of any right triangle can easily be understood or remembered with the acronym, SOHCAHTOA.
SOH => sin(θ) = opposite/hypotenuse
CAH => Cos(θ) = adjacent/hypotenuse
TOA = tan(θ) = opposite/adjacent
Thus, the length of segment BD, in terms of trigonometric ratios for ∆ABD can be done as follows:
Let BD = x
AB = c
AD = b
=>The sine ratio for the length of line segment BD = x, using SOH.
θ = A
Opposite = DB = x
hypotenuse = AB = c
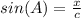
Make x the subject of formula.
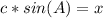
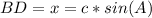
=>The Cosine ratio for the length of line segment BD = x, using CAH
θ = B
Adjacent = DB = x
hypotenuse = AB = c
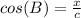
Make x the subject of formula.
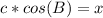
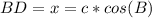
=>The Tangent ratio for the length of line segment BD = x, using TOA
θ = A
Adjacent = DB = x
hypotenuse = AD = b
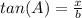
Make x the subject of formula.