Answer:
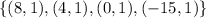
Explanation:
Given
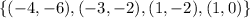
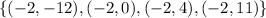
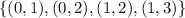
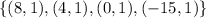
Required
Determine which is a function
A relation is divided into 2; (x,y)
Where x represents the range and y stands for the domain
For a relation to be a function, the x column must be unique; in other words, there must be only one occurrence of x
Testing each of the given options
A.
Start by splitting the relation into x and y columns
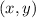


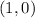
Notice that the third and fourth relation has the same x value of 1;
Hence, this is not a function
B.
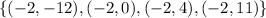
Start by splitting the relation into x and y columns


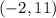
Notice that all relations has the same x value of -2;
Hence, this is also not a function
C.
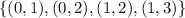
Start by splitting the relation into x and y columns
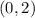
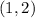

Notice that the first and second relation has the same x value of 0 and the third and fourth relation has the same x value of 1;
Hence, this is also not a function
D.
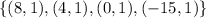
Start by splitting the relation into x and y columns
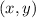
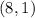
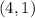
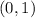

Notice that relation has the unique x values of 8, 4, 0 and -15
Hence, this relation is a function