Question

The data given below consists of the number of children with food allergies at a sample of elementary schools: 3, 9, 5, 5, 14, 10, 5, 11, 9, 6, 1, 8, 10, 7, 9, 13, 18, 9, 8, 11, 9, 7, 6, 14, 12. Find the z-score corresponding to the median of school allergies. You may use your calculator to find the mean and standard deviation.

Answer 1

z -score = 0.0459

Explanation:

Given that:

the number of children with food allergies at a sample of elementary schools: 3, 9, 5, 5, 14, 10, 5, 11, 9, 6, 1, 8, 10, 7, 9, 13, 18, 9, 8, 11, 9, 7, 6, 14, 12.

The objective is to find the z- score , but before we can do that , we need to determine the mean and the standard deviation of the sample.

Mean = sum of the sample/ total number of the sample

Mean = (3+9+ 5+ 5+ 14+ 10+ 5+ 11+ 9+ 6+ 1+ 8+ 10+ 7+ 9+13+ 18+ 9+ 8+11+ 9+ 7+ 6+ 14+ 12)/25

Mean = 219/25

Mean = 8.76

Standard deviation =
`\sqrt{\frac {\sum (x_i - \mu)^2}{N}}`

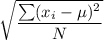
Mean (in order )= 1, 3,5,5,5,6,6,7,7,8,8,9,9,9,9,9,10,10,11,11,12,13,14,14,18)

Standard deviation =
`\sqrt{\frac { (8.76 - 1)^2}{25} + \frac { (8.76 - 3)^2}{25} +\frac { (8.76 - 5)^2}{25} +...+ \frac { (8.76 - 18)^2}{25} }`

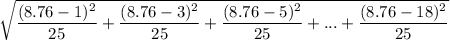
Standard deviation = 5.2174

The standard z score formula is:

`z = (X- \mu)/(\sigma)`

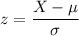
where X = median (13th observation ) = 9

`z = (9- 8.76)/(5.2174)`

`z = (0.24)/(5.2174)`

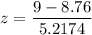
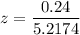
z -score = 0.0459